08. Frenet Coordinates
Frenet Coordinates
Before we discuss process models, we should mention "Frenet Coordinates", which are a way of representing position on a road in a more intuitive way than traditional (x,y) Cartesian Coordinates.
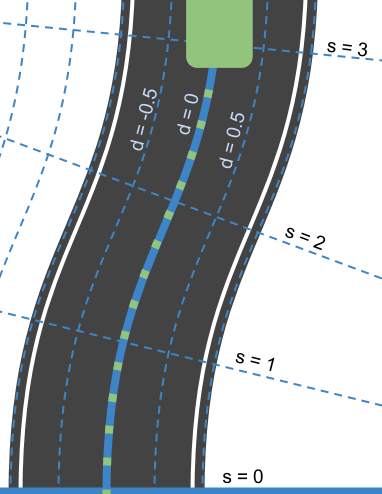
With Frenet coordinates, we use the variables s and d to describe a vehicle's position on the road. The s coordinate represents distance along the road (also known as longitudinal displacement ) and the d coordinate represents side-to-side position on the road (also known as lateral displacement ).
Why do we use Frenet coordinates? Imagine a curvy road like the one below with a Cartesian coordinate system laid on top of it…
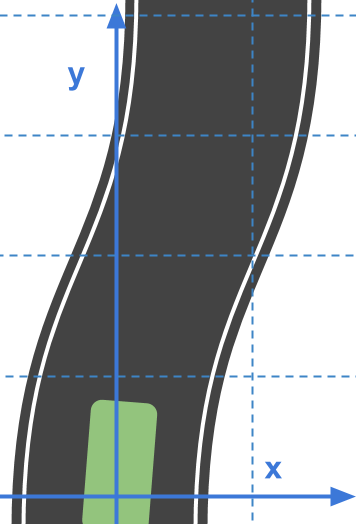
Using these Cartesian coordinates, we can try to describe the path a vehicle would normally follow on the road…
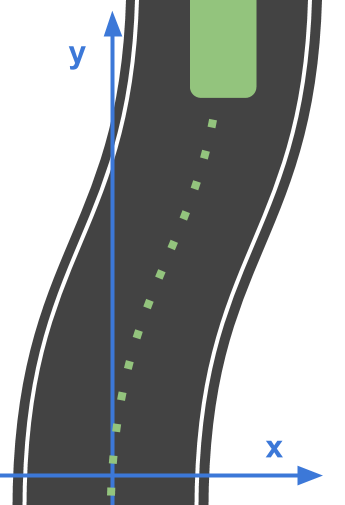
And notice how curvy that path is! If we wanted equations to describe this motion it wouldn't be easy!
x(t) = \text{?}
y(t) = \text{?}
Ideally, it should be mathematically easy to describe such common driving behavior. But how do we do that? One way is to use a new coordinate system. Now instead of laying down a normal Cartesian grid, we do something like you see below…
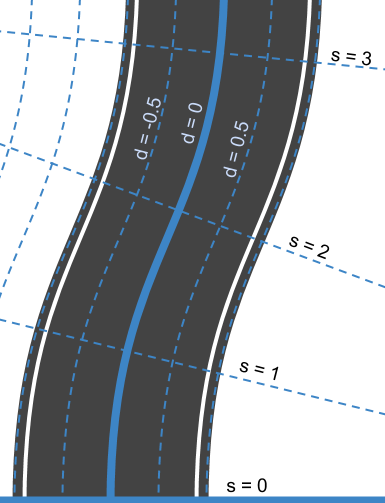
Here, we've defined a new system of coordinates. At the bottom we have s=0 to represent the beginning of the segment of road we are thinking about and d=0 to represent the center line of that road. To the left of the center line we have negative d and to the right d is positive.
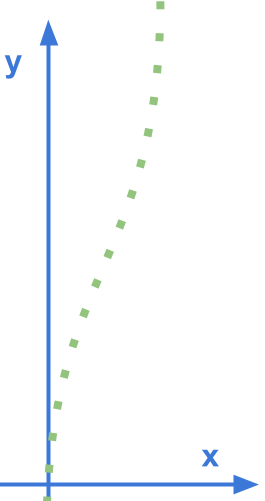
So what does a typical trajectory look like when presented in Frenet coordinates?
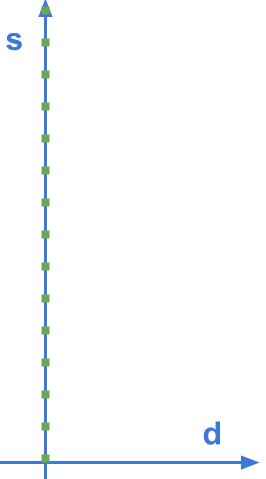
It looks straight!
In fact, if this vehicle were moving at a constant speed of v_0 we could write a mathematical description of the vehicle's position as:
s(t) = v_0t
d(t) = 0
We'll be working with Frenet coordinates a good deal in the rest of the course, because…
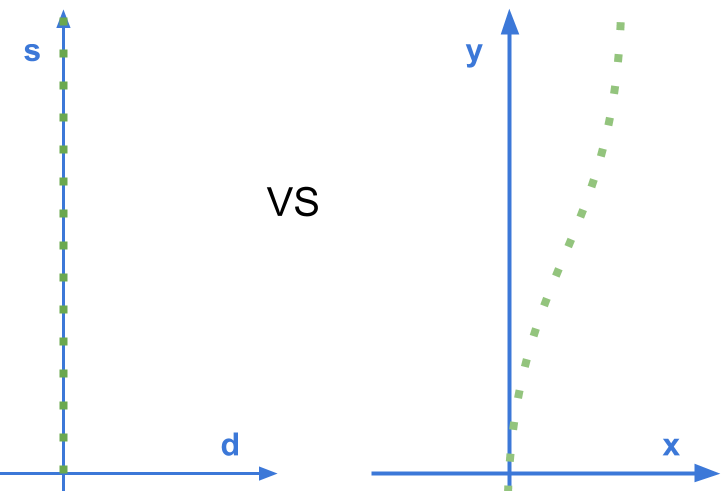
…straight lines are so much easier than curved ones.